Menghitung Ketinggian Orbit Geostasioner pada Objek yang Mengorbit Sebuah Planet

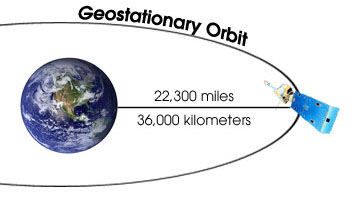
Orbit Geostasioner ( bahasa Inggris: geostationary orbit ) adalah orbit geosinkron yang berada tepat di atas ekuator Planet (garis lintang 0°), dengan eksentrisitas orbital sama dengan nol.

Jika di orbit stasioner tersebut diletakkan sebuah satelit, maka satelit tersebut akan tampak diam terhadap lokasi tertentu di Equator Planet tersebut.

Untuk mencari ketinggian orbit stasioner pada satelit terhadap suatu planet – khususnya bumi – ada pemahaman dasar yang sebaiknya diketahui terlebih dahulu.

Langkah pertama yaitu memahami hukum – hukum dasar Fisika yang berlaku pada benda tersebut. Selanjutnya memahami rumus dasar dan nilai konstanta yang telah ditetapkan oleh Sistem Internasional (SI).

Persamaan dasar yang dipakai dalam bahasan ini :

$\begin{aligned} \displaystyle &1. \textup{ Kecepatan Sudut Rotasi Planet } \omega =\frac{2\pi }{T} \\ \\ &2. \textup{ Kecepatan Linier benda pada permukaan planet } v =\omega R \\ \\ &3. \textup{ Kecepatan Linier benda pada ketinggian } \mathbf{ h }, v_{h} =\omega ( R + h ) \\ \\ &4. \textup{ Percepatan Sentripetal pada permukaan planet } a_{s} = \frac{v^{2}}{R} \\ \\ &5. \textup{ Percepatan Sentripetal pada ketinggian } \mathbf{ h }, a_{sh} = \frac{v^{2}}{( R + h )} \\ \\ &6. \textup{ Gaya Gravitasi pada permukaan planet } F_{G} = G \frac{mM_{p}}{R^{2}} = mg_{p} \\ \\ &7. \textup{ Percepatan gravitasi pada permukaan planet } g_{p} = G \frac{M_{p}}{R^{2}} \\ \\ &8. \textup{ Gaya Gravitasi pada ketinggian } \mathbf{ h }, F_{Gh} = G \frac{mM_{p}}{( R + h )^{2}} \\ \\ \end{aligned}$

Gaya – gaya yang bekerja pada objek yang mengorbit suatu planet

Ilustrasi-Objek-Mengorbit-Planet-pada-Ketinggian-H Untuk mencari perbandingan objek pada ketinggian h dan jari – jari planet, di awali dengan membandingkan gaya – gaya yang bekerja pada objek tersebut, yaitu gaya sentripetal dan gaya gravitasi yang terjadi pada objek di ketinggian h, sebagai berikut :

$\begin{aligned} \displaystyle F_{sh} &= F_{Gh} \\ m a_{sh} &= G \frac{mM_{p}}{( R + h )^{2}} \\ m \frac{v^{2}}{( R + h )} &= G \frac{mM_{p}}{( R + h )^{2}} \\ v^{2} &= G \frac{M_{p}}{( R + h )} \ \ \ ..... \ (9) \\ \\ \end{aligned}$

Dari poin persamaan (3) substitusi ke persamaan (9) menjadi :

$\begin{aligned} \displaystyle (\omega( R + h ))^{2} &= G \frac{M_{p}}{( R + h )} \\ \\ \omega^{2}( R + h )^{2} &= G \frac{M_{p}}{( R + h )} \\ \\ ( R + h )^{3} &= \frac{GM_{p}}{\omega^{2}} \ \ \ ...... \ (10) \\ \\ \end{aligned}$

Substitusi persamaan (1) ke persamaan (10) menjadi :

$\begin{aligned} \displaystyle ( R + h )^{3} &= \frac{GM_{p}}{4\pi^{2}}\cdot T^{2} \ \ \ ...... \ (11) \\ \\ \end{aligned}$

Rasio Jarak Pusat Bumi dan Jari – Jari Planet

Untuk memperoleh perbandingan antara titik orbit dari pusat bumi dengan jari – jari planet, persamaan (11) kita kalikan kedua ruas persamaan tersebut dengan $\frac{1}{R^{2}}$ sehingga menjadi :

$\begin{aligned} \displaystyle ( R + h )^{3} \cdot \frac{1}{R^{2}} &= \frac{GM_{p}}{4\pi^{2}}T^{2} \cdot \frac{1}{R^{2}} \\ \\ \frac{( R + h )^{3}}{R^{2}} &= \frac{T^{2}}{4\pi^{2}} \cdot \frac{GM_{p}}{R^{2}} \ \ \ ...... \ (12) \\ \\ \end{aligned}$

Karena $g_{p} = G \frac{M_{p}}{R^{2}}$ dari persamaan (7), persamaan (12) diringkas menjadi :

$\begin{aligned} \displaystyle \frac{( R + h )^{3}}{R^{2}} &= \frac{T^{2}}{4\pi^{2}} \cdot g_{p} \\ \\ \frac{( R + h )^{3}}{R^{2}} &= \frac{g_{p}}{\pi^{2}} \cdot \frac{T^{2}}{4} \ \ \ ...... \ (13) \\ \\ \end{aligned}$

Persamaan (13) adalah persamaan dari suatu objek yang mengorbit sebuah planet pada ketinggian h.

Ketinggian Orbit Geostasioner Bumi

Kita coba untuk menggunakan persamaan (13), jika planet tersebut adalah bumi. Besar percepatan gravitasi g_p di bumi adalah sebesar 9.8067, sehingga nilai perbandingan antara g_p dan π² adalah :

$\begin{aligned} \displaystyle \frac{g_{p}}{\pi^{2}} = \frac{9.8067}{9.8696} = 0.99363 \approx 1 \end{aligned}$

Dengan demikian persamaan (13) dapat disederhanakan menjadi :

$\begin{aligned} \displaystyle \frac{( R + h )^{3}}{R^{2}} &= 1 \cdot \frac{T^{2}}{4} \\ \\ \frac{( R + h )^{3}}{R^{2}} &= \frac{T^{2}}{4} \ \ \ ...... \ (14) \\ \\ \end{aligned}$

dengan :

R = Jari – Jari Bumi = 6.371.000 meter
T = Periode Rotasi Bumi = 24 jam = 86400 detik
h = Titik Ketinggian Orbit Geostasioner ( meter )

Kita ambil contoh satelit Palapa yang mengorbit Bumi. Dengan R dan T bumi, kita dapatkan :

$\begin{aligned} \displaystyle \frac{( R + h )^{3}}{R^{2}} &= \frac{T^{2}}{4} \\ \\ ( R + h ) &=\sqrt[3]{\frac{R^{2}T^{2}}{4}} \\ \\ ( R + h ) &= 42.311.741,55 \ m \\ \\ h &= 35.940.741,55 \ m \approx 36 \ km \\ \\ \end{aligned}$

Nilai ketinggian ( h ) ≈ 36 km bersesuaian dengan ketinggian satelit Palapa Indonesia yang mengorbit dari permukaan bumi.

Demikian penjelasan beserta penurunan rumus dalam memahami orbit geostasioner ditinjau dari kajian Fisika dan Astronomi. Tulisan ini akan dibahas lanjut pada pembahasan Fisika yang lain khususnya dinamika gaya gravitasi, kinematika gerak melingkar dan momen inersia.

Untuk kondisi planet lain dengan ketinggian orbit stasionernya, bisa menggunakan persamaan (13) secara umum. Untuk contoh penerapannya mungkin akan dibahas pada bahasan yang lain.

Jika ada yang keliru dalam tulisan di atas, mohon agar teman – teman untuk mengkoreksi agar bisa membantu teman – teman yang lain untuk belajar.

Tulisan di atas akan di update jika dirasa perlu untuk ditambahkan baik penjelasan ataupun contoh dalam penerapannya.

Semoga bermanfaat.

Salam 🙂

Sumber Referensi :
» Satelit - Wikipedia Bahasa Indonesia, Ensiklopedia Bebas
» Satelit Palapa - Wikipedia Bahasa Indonesia, Ensiklopedia Bebas
» Geostationary Orbit and Satellites - University of Wisconsin-Madison Space Science and Engineering Center

1729n